The Collatz Conjecture is a well-known enigma. Just a few simple rules seem to connect all natural numbers back to the first number we learn: one. These rules are:
- If the number is odd, multiply it by 3 then add 1
- If the number is even, divide it by 2
For example, the number 3 undertakes a journey like a hailstone tumbling up and down within a thundercloud. Since 3 is odd, we apply rule 1. We get 3*3 + 1 = 10. Now our hailstone gusts up to 10, which is even, so we divide by 2. The hailstone drops down to 5. Applying Rule 1 launches it back up to 16. Since 16 is a power of two, it has become too heavy for the updraft and plummets to the ground via repetitive applications of Rule 2. 16 > 8 > 4 > 2 > 1. The numbers visited by a hailstone on its journey to the ground are known as a hailstone sequence.
Doing this process for any natural number seems to lead back to 1. This observation is called the Collatz Conjecture. Finding a proof is a famous unsolved problem in mathematics. Why is this so? Does it hold for ALL natural numbers? Questions like these are beyond my mathematical chops, but the conjecture does make neat fodder for visualization.
Obviously, there should be arrows between numbers and their next Collatz numbers. It is much less clear where to position these numbers. We could put them on a number line, but the edges would get jumbled quickly.
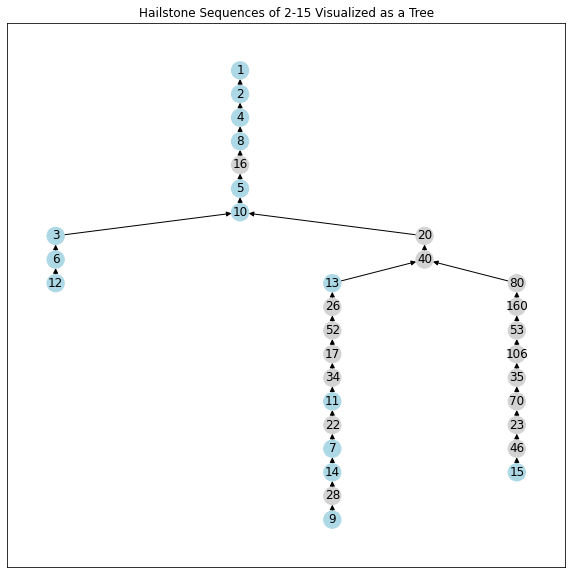
We could structure it as a tree, but the numbers would lose their natural ordering.
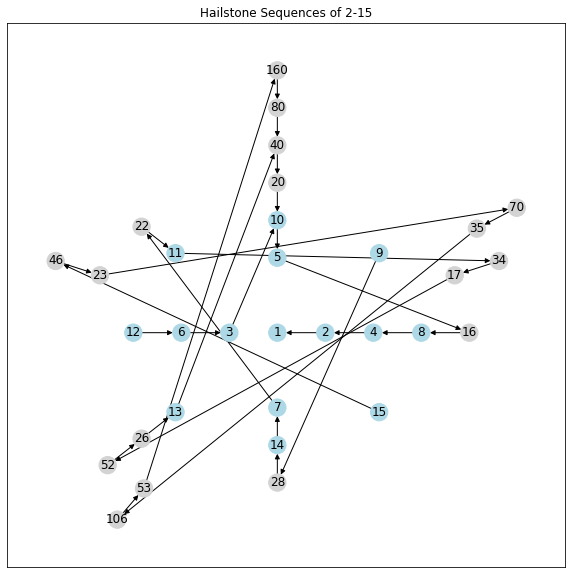
Since the powers of two are the highway to 1 (as seen at the top of the tree), it is essential to preserve this in the visualization. I settled on nesting doubling rings. The innermost ring would consist of just 1. The next ring is 2 and 3. After that, 4, 5, 6, and 7. Each successive ring has twice as many numbers as the ring before it. Each number is interpolated evenly along its ring. This helps ensure the powers of 2 are neatly lined up. With this arrangement in mind, the below image shows the hailstone sequences for 2-15. Intermediate numbers visited by hailstones are colored gray.
To get a number’s corresponding Cartesian coordinates, I derived these equations that map a natural number to its polar coordinates. From there, it’s easy to switch into Cartesian:
$$f \colon \N \rightarrow \N \times \R \rightarrow \R^2 \\
n \mapsto (r_n,\theta_n) \mapsto (x_n, y_n) \\
r_n = \lfloor \log_2n \rfloor \\
\theta_n =2\pi \frac{n-2^{r_n}}{2^{r_n}} \\
x_n = r_n \cos \theta_n \\
y_n = r_n \sin \theta_n$$
Intuitively, the equations “slice” the number line into chunks separated by powers of two, then “wrap” these chunks into appetizing 2D donuts of numbers! Using this method of mapping any natural number to the 2D plane makes drawing a whole lot easier. The 2-smooth
Applying the connections of Collatz to this nesting arrangement of doubling rings yields a fascinating picture, especially as we crank up the size to 1024 hailstone sequences. For clarity, only odd-even edges are shown.
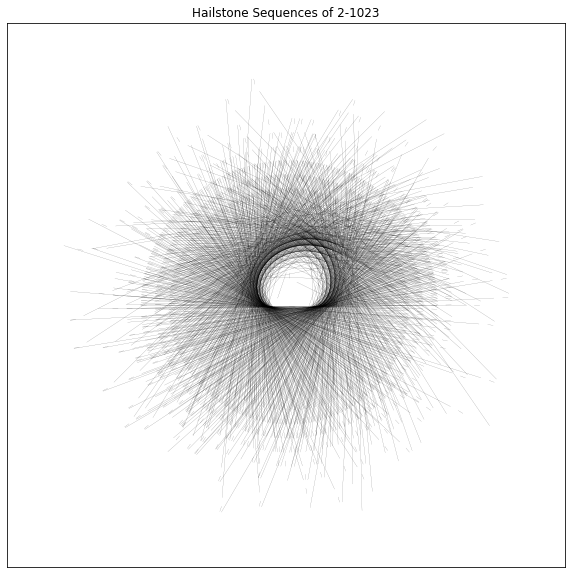
What is that onion-like structure? A closer look:

Why don’t any lines dare cross the center? This visualization just brings up more questions than answers. But for now, it’s cool to enjoy how donuts can yield an onion. (OK, that wasn’t very appetizing).
Problems with this visualization include running out of space (successive circumferences don’t double). These issues and other considerations are addressed in Part 2, another post for another day. If you want to play around with these visualizations, here’s my Python code.

Comments are closed.