Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
How many such routes are there through a 20×20 grid?
https://projecteuler.net/problem=15
This problem is actually pretty cool – it doesn’t need any programming to solve. Well, maybe a calculator. At first glance, this problem might seem difficult to solve analytically. But it is not so! An important technique in problem solving is reducing problems to sub-problems. Let’s consider the lattice paths of the 1×1 grid.
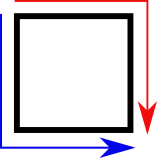
There are two paths. That was easy! Now, let’s consider the 2×1 grid. One movement to the right reduces the problem to just the 1×1 grid, which we know has two paths to the bottom right corner. There is only one other open route. So for the 2×1 grid, there are 2+1=3 paths. This is also true for the 1×2 grid by way of symmetry. It’s also easy to see that any \(n \times 1\) or \(1 \times n\) grid will have \(n+1\) paths.
Using just those pieces of information, let’s look at the 2×2 grid. One movement to the right reduces the problem to the 1×2 grid. One movement down reduces the problem to the 2×1 grid. Both of these sub-grids have 3 paths to the bottom right corner. Therefore, the 2×2 grid has 3+3=6 paths.
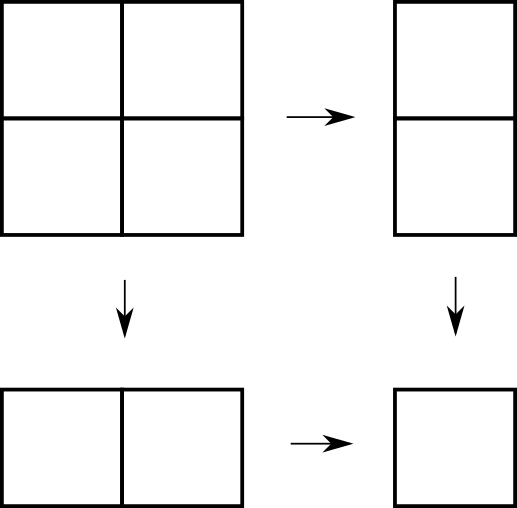
The pattern is now clear. Bigger and bigger grids’ solutions can be constructed in a fashion similar to Pascal’s Triangle, by adding together both sub-grids’ number of paths. In the example below, the solution for \(4\times4\) is \(70\).
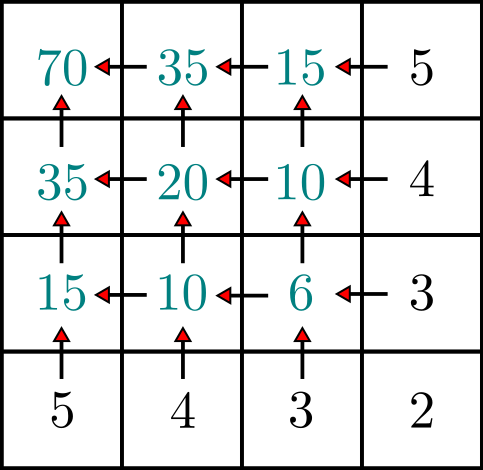
This can be extended all the way to 20×20, but the numbers quickly get unwieldy to add together. Can an analytical solution, rather than a recursive solution, be found? Let’s take a different tack and come at this from a combinatorics angle. A path in the \(n \times n\) grid has \(2n\) junctions. A movement down will eventually force a movement to the right, and vice versa. This means that only half of the junctions can be assigned to one movement. The other half of the junctions has to be assigned to the other movement.
Taking a route across the grid is actually choosing \(n\) junctions, out of \(2n\) junctions, to be assigned to a specific movement. Order of these assignments doesn’t matter. The number of combinations is a binomial coefficient with \(2n\) choose \(n\). Plugging these into the formula for a binomial coefficient results in
$$\binom{2n}{n}=\frac{(2n)!}{(n!)^2} \tag{1}$$
Just slap \(n=20\) down in Equation 1 and calculate.
$$\frac{40!}{20! \times 20!}=137846528820$$


Comments are closed.